Introduction

I’ve recently inundated myself with interview preparation. Along the way, I thought a lot about how to intuit runtime complexities for various algorithms. I thought that it might be nice to cement it all with an article - both for the sake of others, as well as for my sake. This is the first article in that vein, strictly dealing with binary search trees.

Terminology

Note: This article frequently uses the abbreviation BST to describe binary search trees.

Here are properties of trees that this article deals with:

  • Number of nodes in a tree is typically denoted n.
  • Height of a tree is typically denoted k.
  • Complete: every level except possibly the last is completely filled.
  • Full: every node has 0 or 2 children. This is a subset of complete: every full tree is a complete tree.
  • Balanced: the height of the left and right subtrees of every node differ by at most 1. Using the root node as our focus, we can intuit that any balanced tree has fairly uniform height.
  • Binary Search Tree: A tree in which each element to the left of a node is guaranteed to be less, and to the right guaranteed to be greater. BSTs may not be balanced.
  • Red-black Tree: A BST that is balanced.
  • AVL Tree: A BST that is balanced (in a different way than red-black trees).
  • Branching factor: The number of children at each node.

Searching a BST

Everyone knows that searching a binary search tree has runtime complexity O(logn), right? …right? Let’s take a second to tease apart some questions from that assertion to see if we really understand what we mean when we say that:

  • Q: What is the base of the log?

    A: Typically when we talk about the base of a log, we’re talking about 2 or 10. In the case of a BST case it’s 2 (we’ll dive into why that is shortly).

  • Q: What does n represent?

    A: n usually means “number of elements”. In this case, n does mean that: or, another way to put that is “number of nodes in the tree”.

So, expanding O(logn), we have: O(log2(<# nodes in tree>)).

Well, searching a BST is not strictly O(log2(n)): it depends on whether the BST is balanced or not. An unbalanced BST may be O(n). Let’s discover why by exploring how the log2 comes about.

Logarithms and exponents

Let’s look at the following full binary tree:

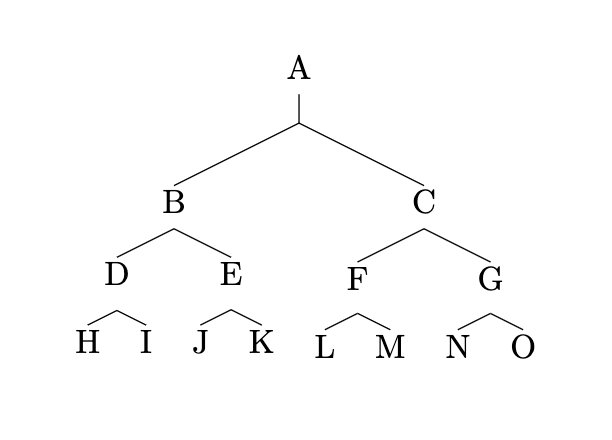
Full Binary Tree

We can tell the following about this tree:

  • It has height k=4.
  • It has nodes n=15.

The number of nodes is the sum of the nodes at each level. The number of nodes at each level are powers of 2. So, at k=4 there are,

\[\begin{align*} n=1+2+4+8 && \text{The sum of the nodes at each level.} \\ n=2^0+2^1+2^2+2^3 && \text{Represented in powers of 2.} \\ n=\sum\limits_{j=0}^{k-1} 2^j && \text{Represented as a summation.} \\ \end{align*}\]

The branching factor here is 2 - each node has 2 children. What if each child had 7 children, or 9, or 21? Let’s re-write the summation with a generic branching factor b:

\[\begin{align*} n=\sum\limits_{j=0}^{k-1} 2^j && \text{Branching factor of 2, as before.} \\ n=\sum\limits_{j=0}^{k-1} b^j && \text{Branching factor of b.} \\ \end{align*}\]

Sums are a bit of nuisance. Let’s convert this sum into a discrete formula:

\[\begin{align*} n=\sum\limits_{j=0}^{k-1} b^j \\ n=b^{k-1}+b^{k-2}+...+1 && \text{Expanding the sum.} \\ n \cdot b=(b^{k-1}+b^{k-2}+...+1) \cdot b && \text{Multiply by b.} \\ n \cdot b=b^k+b^{k-1}+...+b && \text{Distribute the b into the sum.} \\ n \cdot b + 1=b^k+b^{k-1}+...+b+1 && \text{Add 1 to each side.} \\ n \cdot b + 1=b^k + n && \text{Note that we can use n for the right side.} \\ n \cdot b - n=b^k - 1 && \text{Move n left; 1 right.} \\ n \cdot (b - 1)=b^k - 1 && \text{Factor out n.} \\ n = \frac{b^k - 1}{b - 1} && \text{Divide by n-1.} \\ \end{align*}\]

Let’s test the formula by using k=4 and b=2 again, which we think should equal n=15:

\[\begin{align*} n=\frac{2^4-1}{2-1} \\ n=\frac{16-1}{1} \\ n=15 \\ \end{align*}\]

What if we knew the amount of nodes, but not the height? We can rework the formula we just came up with to give us height using number of nodes,

\[\begin{align*} n=2^k-1 \\ n+1=2^k && \text{Move 1 to the left.} \\ \log_2 {(n+1)}=\log_2 {(2^k)} && \text{log2 both sides.} \\ \log_2 {(n+1)}=k \cdot \log_2 2 && \text{Power rule.} \\ \log_2 {(n+1)}=k && \text{Identity rule.} \\ k=\log_2 {(n+1)} \end{align*}\]

Back to binary search trees

How can we apply this knowledge? Consider again our original topic of a binary search tree: one property of a BST is that a search operation requires no backtracking. That is: the path to a node always going to go at most to a leaf node - it never reaches a leaf and then has to backtrack and try a different choice at a former node.

If the BST is unbalanced, the worst case time complexity to search for a value is O(n). We can easily show that this is the case with the following tree:

Left BST

This BST is heavily weighted to the right. To search for the value 109, we’d have to look at each of the n=15 elements. That is: the worst case time complexity is O(n).

What if this BST were balanced, instead?

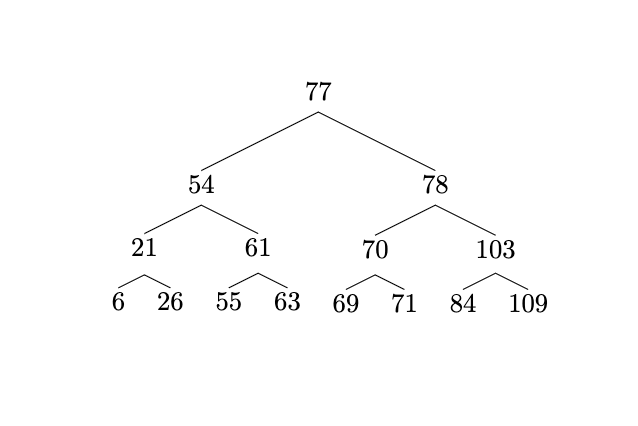
Balanced BST

Now, to search for any value in the BST, the maximum depth we’d need to traverse is k. We know that k=log2(n), so we can say that the big-O runtime complexity in terms of n is O(log2(n)).

In conclusion

There are at most n=(b^k - 1)/(b - 1) nodes in any tree with height k and branching factor b. In a binary tree, that simplifies to n=2^k-1, and can be re-written in terms of height as k=log2(n+1).

To conclude our original question: binary search trees don’t guarantee O(log2(n)) search: balanced BSTs do.

In a future article we’ll look at Heap runtime complexity, and how memoization affects that. In some other future article we’ll look at backtracking and permutation runtime complexities.